Are African Prices Too High?
A Balassa-Samuelson-Based Hot Take
Why is African manufacturing failing to take off?
Manufacturing in Sub-Saharan Africa is stuck at less than 10% of GDP, compared to 24% in East Asia and even 17% in Latin America and the Caribbean. Any discussion of a China-style takeoff in the region is a nonstarter without understanding what is holding back manufacturing.
A plausible answer to this question comes from this 2013 paper by Alan Gelb, Christian Meyer, and Vijaya Ramachandran at the Center for Global Development. They argue that though African countries are quite poor, African factory workers’ wages are relatively high. More specifically, industrial labor costs in Africa are high compared to non-African countries at similar levels of GDP. In this sense, paradoxically, “poor does not mean cheap”.
Okay, then, that raises the next question. Why are industrial labor costs relatively high in Africa?
Gelb, Meyer, and Ramachandran argue that surely it has something to do with prices. If African prices are high, relatively high wages might make sense, to cover living costs.1
Shifting the puzzle from high wages to high prices seems to kick the can down the road one more time: but here at least I think there’s some intellectual progress to be made with a little application of old-school trade theory. This is my attempt at a short and unabashedly econ-wonky post, in the proud tradition of vintage 2010s-era Krugman / DeLong / Smith. More literary programming will return in the following weeks.
Poor Does Not Mean Cheap
Here’s a depiction of the problem of “high African prices” in graph form.
Gelb, Meyer, and Ramachandran plot the classic Balassa-Samuelson relationship: real GDP on the x-axis, price level on the y-axis, with each country in the Penn World Tables a single point. This should tell us if prices are relatively high in Africa for a given level of GDP:
Lo and behold—sub-Saharan African countries, that cluster of red dots, all largely lie above the red line of best fit. So for a given level of GDP, African countries have higher prices than a linear model would predict for the rest of the world.
Another way to visualize this is by plotting the residuals, the vertical distance between each country’s price level and their price level predicted by the Balassa-Samuelson line of best fit:
There’s a lot of red at the top of that graph: African countries really seem to have prices that are too high compared to the linear fit.
We’ve replaced one puzzle with another, and another again. What was once a puzzle about Africa’s low manufacturing shares and then a puzzle about manufacturing wages is now really one about African prices being too high relative to the Balassa-Samuelson relationship. The great Pseudoerasmus opines that this seems like a neglected puzzle to solve for growth and development.
But is there really a puzzle at all?
A Quick Balassa-Samuelson Recap
Let’s rewind a bit here and think through some of the fundamentals. (Feel free to skip to *** if you don’t like math.)
The Balassa-Samuelson relationship falls out of a simple two-country, two-sector neoclassical model.
Let’s say there are two countries, A and B. Each economy has two sectors: tradable and non-tradable. For simplicity, let’s say labor is the only factor of production. For even further simplicity, let’s set the marginal productivity of labor in the non-tradable sector in countries A and B both equal to 1,
where the subscript NT means “non-tradable” and A and B are the countries.
Since we’re in Neoclassical Land, workers are paid their marginal product of labor times the price in the tradable sector:
and in the nontradable sector too (which we can simplify since MPL_NT=1):
Thus, wages equal the price of the non-tradable good. Workers are also free to move between the tradable and non-tradable sectors, which equalizes the wage between T and NT, but not between countries. And the price of the tradable, being tradable, is equalized across countries. Putting this all together and solving for the ratio of non-tradable prices between A and B gives
Let’s assume, without loss of generality, that country A is richer and more productive than B, i.e. MPL_{T,A} > MPL_{T,B}. Then the price of non-tradables in country A is going to be higher than in B, and thus the price level in country A is also going to be higher than in B.2
*** This tiniest of models gives us the Balassa-Samuelson prediction shown in that scatter plot: richer, more productive countries should have higher prices. Poorer countries should have lower prices. The line of best fit should slope upwards.
Intuitively, what’s going on is that higher productivity in rich countries increases wages for both the tradable and non-tradable sectors, making everything more expensive. When factory wages go up because of technological progress, this also pulls up the wages of hairdressers and barbers, raising prices for everyone.
Now we should ask—where’s the model going wrong?
One Man’s Points-Lying-Above-A-Line is Another Man’s Nonlinearity
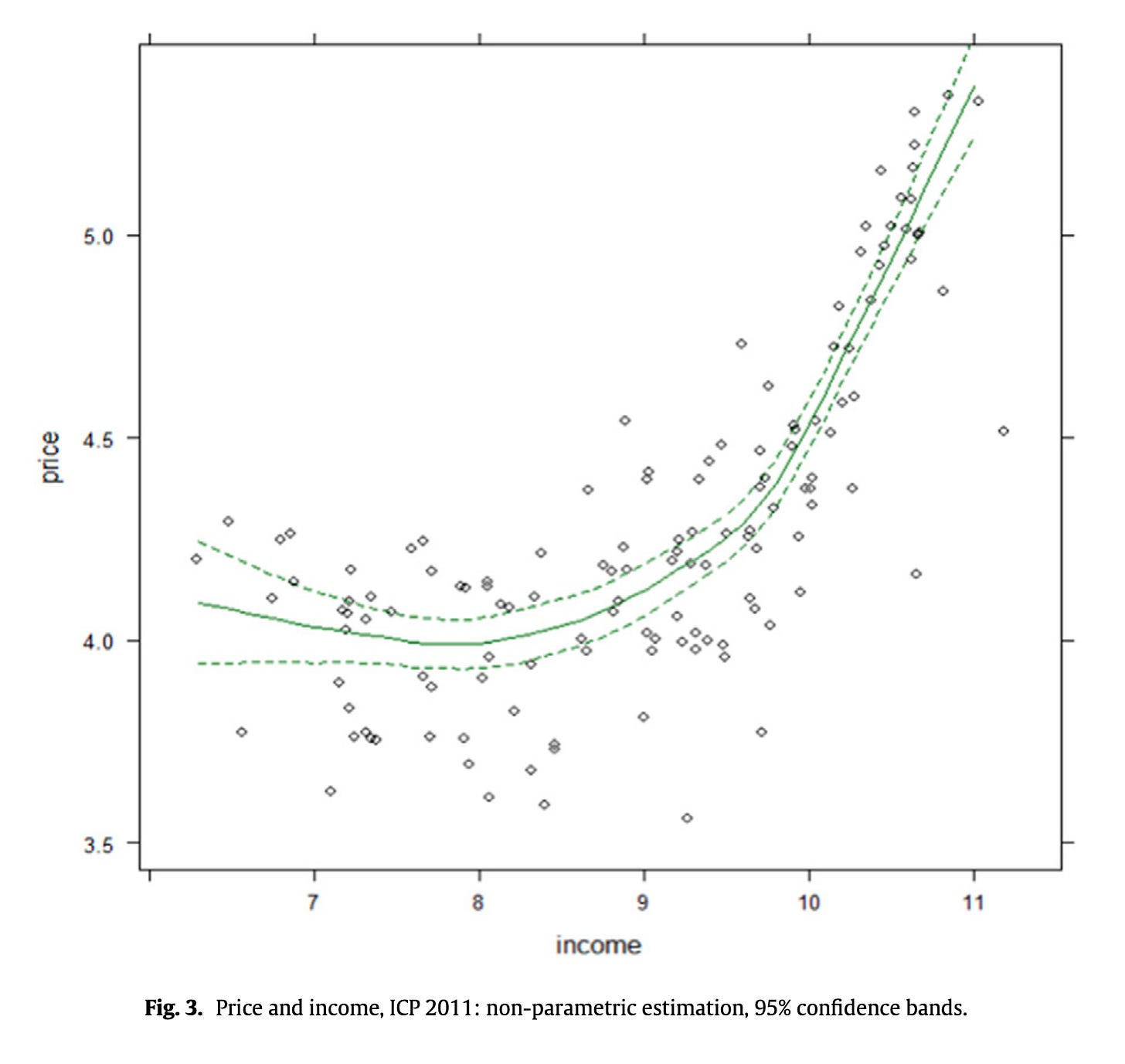
Hassan (2016), which I think is a severely underrated paper, starts out with the acute observation that maybe the price level-GDP relationship isn’t a linear relationship at all. Here’s his version of the scatter plot using a 2011 cross-section of countries:
If you scroll back up to the original Gelb et al chart and squint, you can make out the same banana shape. One man’s points-lying-above-the-line is another man’s nonlinearity.
Hassan lays out a simple model to explain this U shape, which I think captures a key feature of the world missing in the simple Balassa-Samuelson model.
When thinking about the differences between rich countries, middle income countries, and the poorest countries, dividing the economy into two sectors—Tradable and Non-Tradable—like the Balassa-Samuelson model isn’t the most obvious way to slice things. Instead, in development, we typically think of three big sectors: agriculture, manufacturing, and services. The story of development is largely the story of structural transformation between these three sectors: the poorest countries farm; middle-income countries like China and Mexico manufacture goods; and most of the rich West does services.
How do these three sectors map onto the Tradable vs. Non-Tradable distinction? Manufacturing is obviously tradable. Services are obviously non-tradable. But agriculture is a mixed bag. Hassan chooses to model it as non-tradable: in practice, most of the poorest countries survive on subsistence agriculture, and hardly trade their agricultural produce at all. And for the richest countries, agriculture ends up being a relatively minor component of both output and the price basket anyway.
In other words, contrary to the baseline Balassa-Samuelson setup, developing economies go from non-tradables to tradables and then back to non-tradable services again, once they’re really rich.
These assumptions, and a little algebra, yield the augmented Balassa-Samuelson equation:
which, when fed data on labor shares l, expenditure share γ, and productivity A, voila, predicts the observed nonlinear relationship between price and GDP:3
Intuitively, poorer countries have more of their labor forces and consumption baskets tied up in non-tradable subsistence agriculture, so when agricultural productivity grows, it lowers the price level—the exact reverse of the conventional Balassa-Samuelson relationship. But at some point, enough people have moved into manufacturing that agricultural productivity growth becomes less relevant, and the traditional upward-sloping Balassa-Samuelson relationship reasserts itself. Hence: a U-shape between incomes and prices.
The Upshot for African Prices
We’ve taken a long detour from the original goal, understanding if African industrial labor costs are relatively high. Let’s bring it back.
In their CGDev paper, Gelb et al. argue that perhaps there are Africa-specific explanations for why African countries appear to have relatively high prices—these might include natural resource exports or aid. What Hassan (2016)’s model shows is that it’s possible to explain why African prices are high relative to GDP, without needing to add an epicycle specifically for Africa. (Gelb et al. also ultimately land at a similar place, positing that it likely has to do with low-productivity but high-employment agriculture.)
The clincher for me is actually less Hassan’s model, which shows one simple mechanism that is consistent with the data (albeit one more realistic than baseline Balassa-Samuelson). It’s what happens when Hassan plots prices against incomes from 1950 to 2011 as a panel, and not just in a single cross-section of time:
There’s that familiar U-shaped pattern again.
Perhaps African prices aren’t so high after all. What may seem at first a problem unique to Africa may simply be a reflection of a common experience of all developing countries as they undergo structural change.
Postscript (12/8/2024)
There was some Twitter discussion after the original post, asking: if all the points on the leftward points on the “U” (i.e., the poorest countries) are African, is the puzzle preserved?
Without good long-run panel price data, this will remain something of an open question. But since the World Bank released its 2021 International Comparison Program data I decided to take it for a spin. Below are my replications of the Hassan regression using the 2017 and 2021 vintages of the data:
The left two columns are with the linear Balassa-Samuelson, and the right two are with the quadratic term added. The key takeaway is that the Africa indicator disappears with the addition of the square term.
It’s not conclusive, but it suggests there’s juice in the nonlinear Balassa-Samuelson view.
Prices and wages are clearly jointly determined in general equilibrium; but let’s put this issue aside for now and start by understanding prices.
When thinking about the overall price level, we don’t need to worry about the tradable good since the price is the same across both countries.
As an aside, Hassan’s results imply that Chinese renminbi was 30% less undervalued than a conventional linear Balassa-Samuelson relationship would suggest. The same is likely true for other “devalued” East Asian exporters, complicating the findings of the influential Rodrik (2008), which found strong pro-growth arguments for devaluation.










For now Africa should focus more on developing agriculture instead of manufacturing. Most of them have same cereal yields per hectares since decolonisation.
Unreliable energy makes manufacturing impractical.
Just as Germanys green energy polices are killing German manufacturing, high energy cost and low energy reliability prevents Africas manufacturing from taking off.